Carry Cancel Adders

There are plenty of ways to optimize an adder. As you may have noticed, it is quite tedious to sequentially use full adders in Minecraft. There are compact builds of course, but is there any other way to efficiently add two binary inputs?

It turns out there are many, but one of them we are going to discuss is called the carry cancel adder. Observe that when we added two binary numbers, we used two half adders. This is synonymous to the output sum bit being equivalent to using XOR on input1, input2, and carry. Try it yourself:

                     1  <- input carry
                     0
                     1
                     -
    output carry <- 10  
        

This means all we need to worry about is finding those carries at each step, right? If you notice, when the two inputs are BOTH one (e.g., 1 + 1 = 2 or 10 in binary), a carry gets propagated. That carry "signal" is propagated as long as higher inputs also contain ones. For example:

     111111111
     1010101011
     0101010101
    -----------
    10000000000
        

Thus, when we see two ones, we produce a carry signal. We stop carrying (if you guessed it) when we see two inputs that are BOTH 0. Note that the signals are shifted one to the left (just like carries are shifted one to the left):

    00111
    010011
    100101
    ----------
    111000
        

Carry cancel adders are synchronized adders because they receive all their carries at the same time and produce outputs accordingly. The full adder from the previous module (also known as a ripple carry adder) must propagate carries to other inputs first before an nth-place in a number can be calculated. This is significantly faster for 8-bit addition. We will use the CCA in compact builds moving forwards. Given all of this, take some time to understand the following logic diagram.

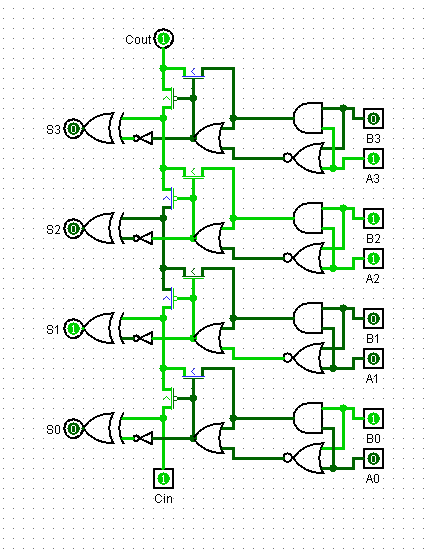
The below is a representation of the carry-cancel propagation. We utilize a glass tower to transmit a signal upwards, and the comparator can choose to cancel the signal at some point moving upward. The signal going through the back of the comparator is a carry signal at the nth digit, and the signal going through each side of the comparator is a cancel signal at the nth digit. Once you determine how to produce these signals given two inputs at some digit i, you can create a full CCA. Note, we will probably give you the schema for the CCA, but you should understand how this works.